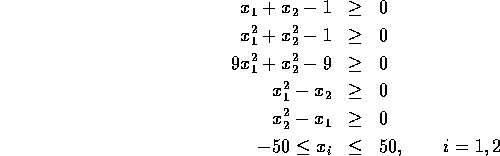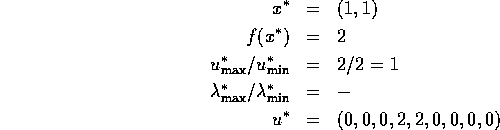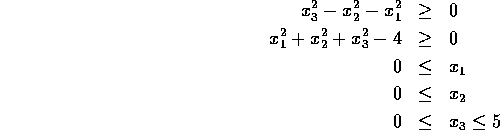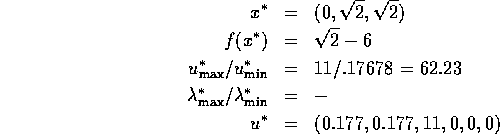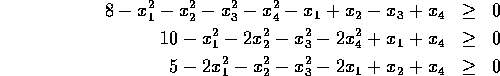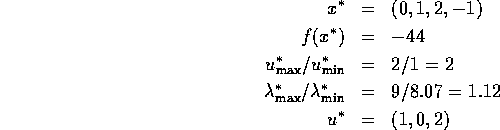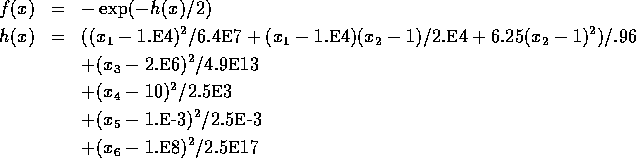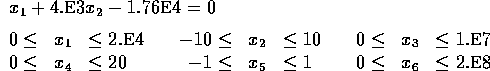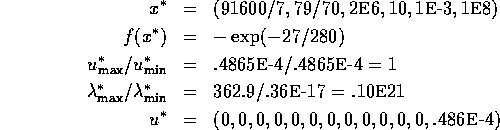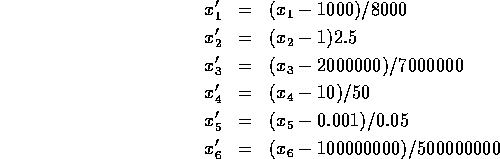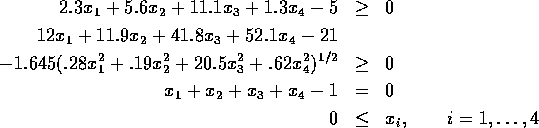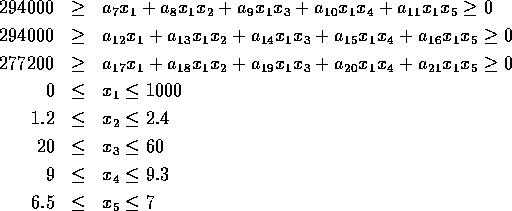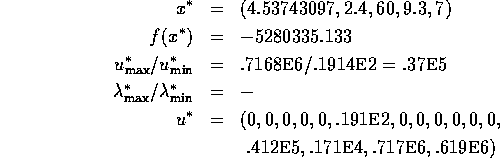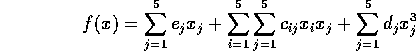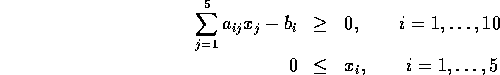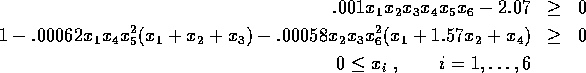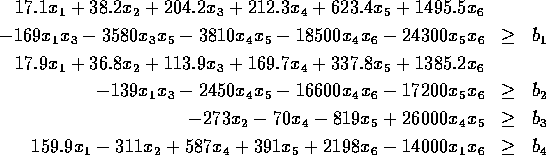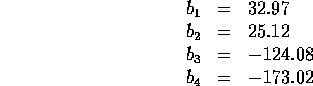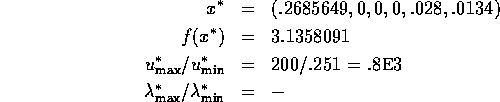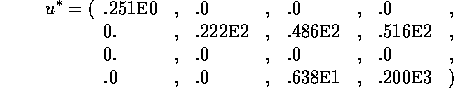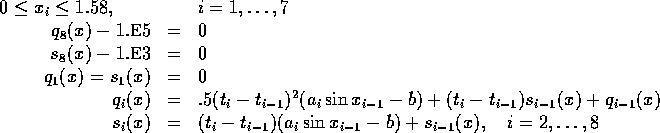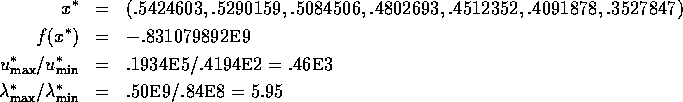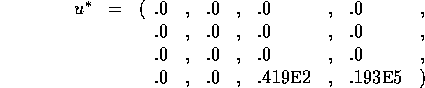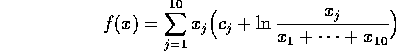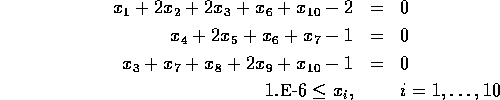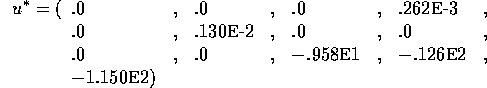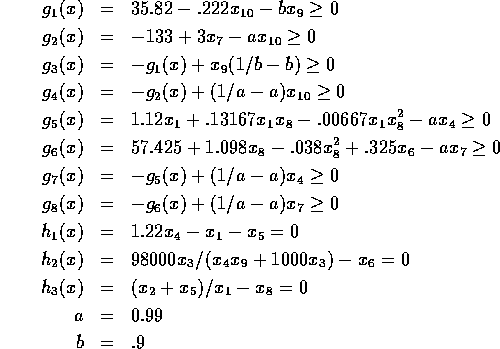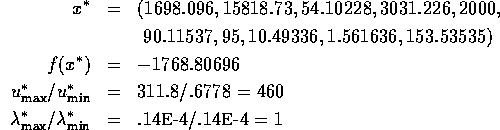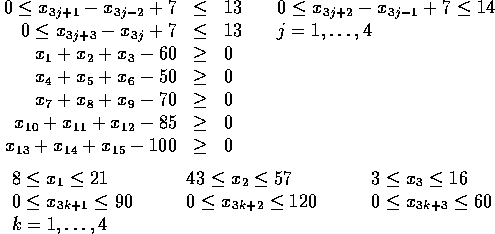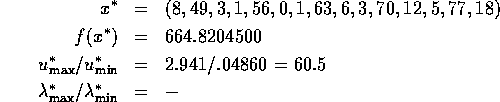Problembeschreibung -- restringierte Optimierung
Dies ist eine kleine Sammlung von Testfällen aus W. Hock, K. Schittkowski:
Test Examples for Nonlinear Programming Codes.
Lecture Notes in Econ and Math. Syst. 187
In der folgenden Liste sind die folgenden Problemdaten beschrieben:
-
Die das Problem festlegenden Funktionen
-
Standardstartwert.
Dieser kann in der Eingabe verändert werden. Bei einigen der Algorithmen
ist der Standardstartwert abgeändert, um Zulässigkeit zu erreichen.
-
Lösung.
Die Genauigkeit der Lösung ist nicht in allen Fällen mit der angegebenen
Stellenzahl garantiert.
-
Das Verhältnis von betragsgrößtem zu betragskleinstem Multiplikator
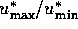 ungleich null.
Die Lösung wird mit wachsendem Wert schwieriger.
ungleich null.
Die Lösung wird mit wachsendem Wert schwieriger.
-
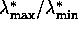 ist die Konditionszahl
der projizierten Hessematrix, also des auf die korrekte Randmannigfaltigkeit
restringierten Problems. Dagegen ist die Matrix
ist die Konditionszahl
der projizierten Hessematrix, also des auf die korrekte Randmannigfaltigkeit
restringierten Problems. Dagegen ist die Matrix

selbst
nicht in allen Fällen definit.
Mit zunehmender Kondition wird die numerische Lösung des Problems immer
schwieriger.
Ist dort ein ``-'' angegeben, so bedeutet dies, daß die Lösung in einer
Ecke liegt, was die Problemlösung sehr erleichtert.
Problem 23
Number of variables: n=2
Objective Function:

Constraints:
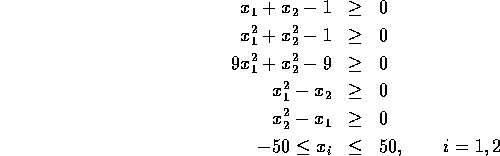
initial guess:

Solution:
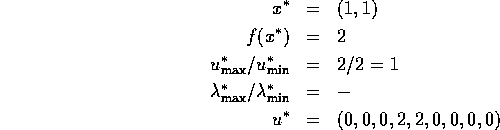
Problem 33
Number of variables: n=3
Objective Function:
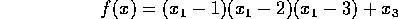
Constraints:
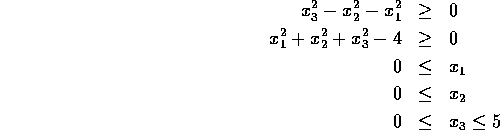
initial guess:

Solution:
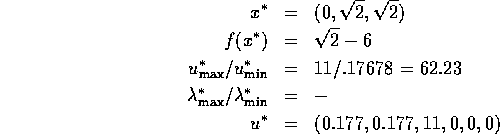
Problem 43 (Rosen-Suzuki)
Number of variables: n=4
Objective Function:
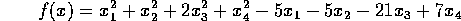
Constraints:
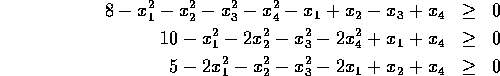
initial guess:

Solution:
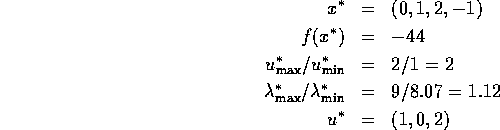
Problem 54
Number of variables: n=6
Objective Function:
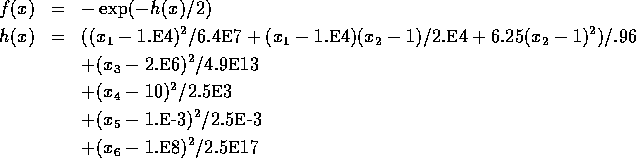
Constraints:
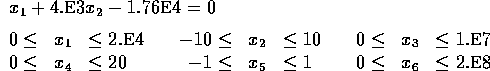
initial guess:
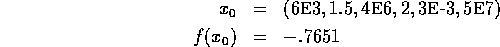
Solution:
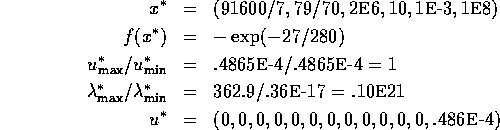
hs54scal entsteht aus diesem Problem durch die Transformation
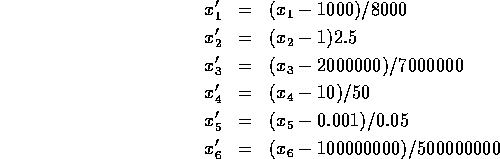
Dieses Problem ist sehr leicht lösbar.
Problem 73 (cattle-feed)
Number of variables: n=4
Objective Function:
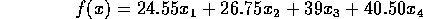
Constraints:
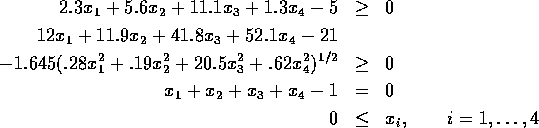
initial guess:

Solution:

Problem 84
Number of variables: n=5
Objective Function:
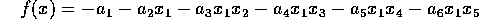
Constraints:
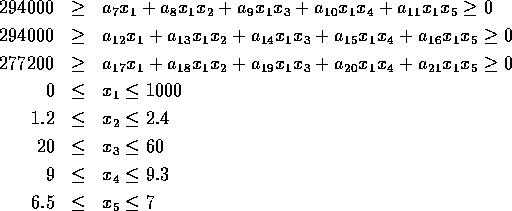
The coefficients 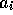 may be drawn from the following table:
may be drawn from the following table:
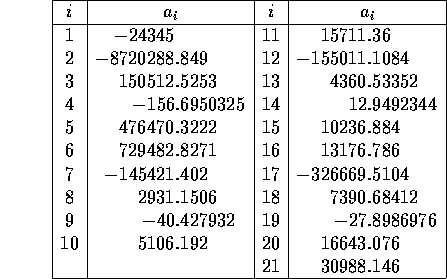
initial guess:
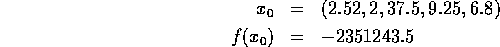
Solution:
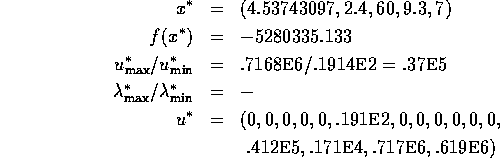
hs84scal entsteht aus diesem Problem durch die Transformation
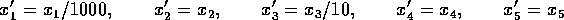
und Division der ersten drei Ungleichungen durch 1000.
Problem 86 (Colville No. 1)
Number of variables: n=5
Objective Function:
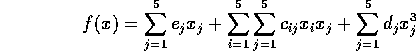
Constraints:
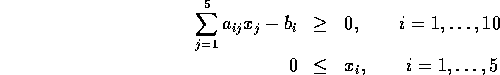
The coefficients 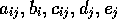 may be drawn from the
following table:
may be drawn from the
following table:
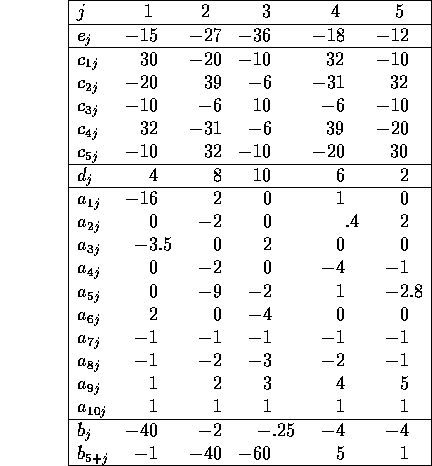
initial guess:

Solution:

Problem 93 (transformer design)
Number of variables: n=6
Objective Function:
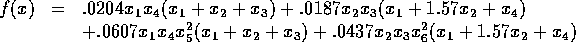
Constraints:
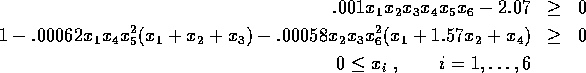
initial guess:
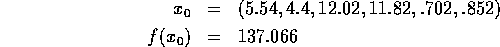
Solution:

Problem 98
Number of variables: n=6
Objective Function:
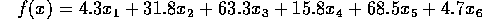
Constraints:
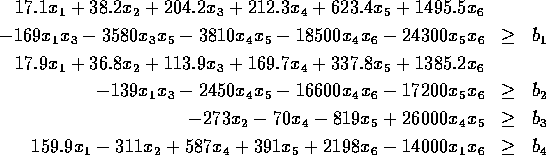
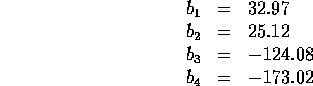
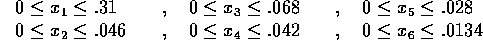
initial guess:

Solution:
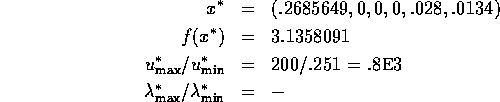
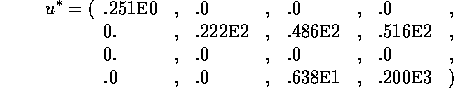
Problem 99
Number of variables: n=7
Objective Function:

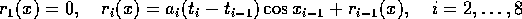
Constraints:
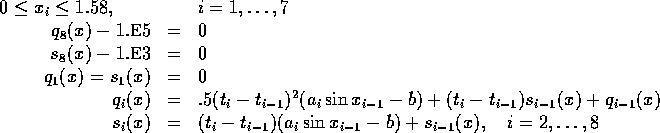
The coefficients 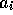 and
and 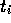 are
are
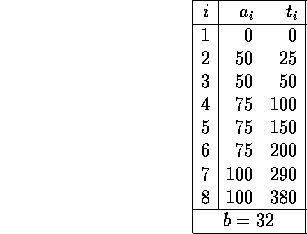
initial guess:
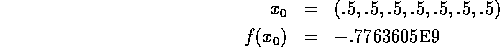
Solution:
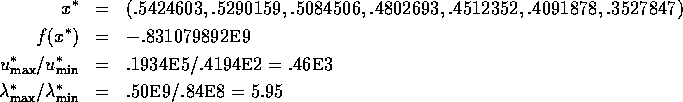
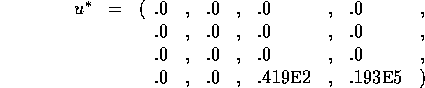
hs99scal entsteht aus diesem Problem durch die Transformation
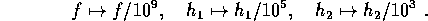
Problem 112 (chemical equilibrium)
Number of variables: n=10
Objective Function:
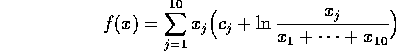

Constraints:
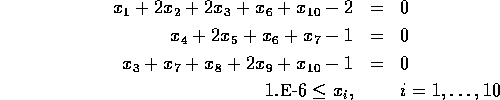
initial guess:

Solution:

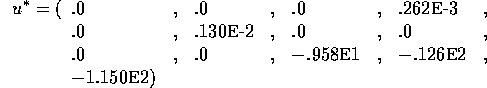
Problem 114 (alkylation process)
Number of variables: n=10
Objective Function:
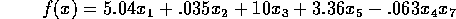
Constraints:
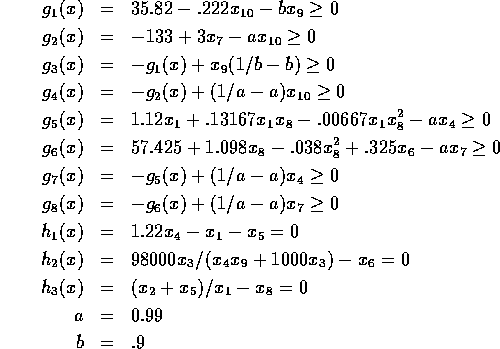
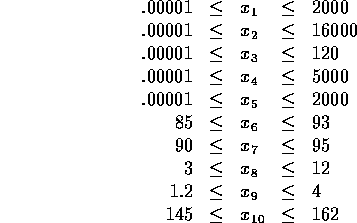
initial guess:
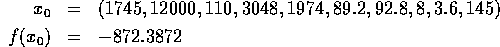
Solution:
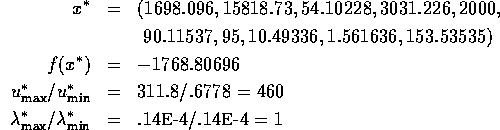

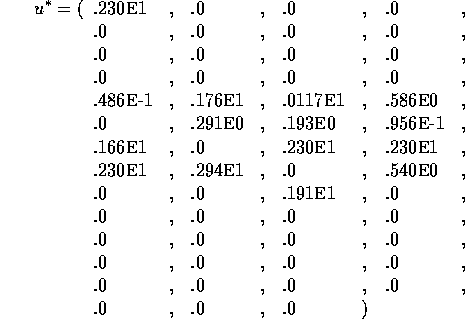
Problem 118
Number of variables: n=15
Objective Function:
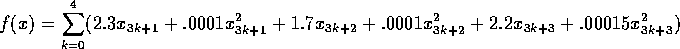
Constraints:
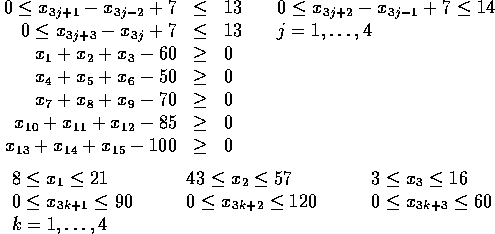
initial guess:
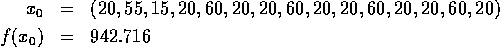
Solution:
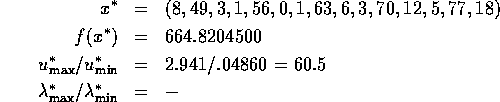
Peter Spellucci
Mon Jun 8 17:36:34 MESZ 1998
|
|
|
|
|
Back to the top!
14.04.2000
|
|
|
|
|