No Title

Examples of unconstrained optimization problems

Most of these problems are taken from the collection of Morè, Garbow, and Hillstrom, ACM TOMS vol. 7 no. 1 (march 1981) 17-41.

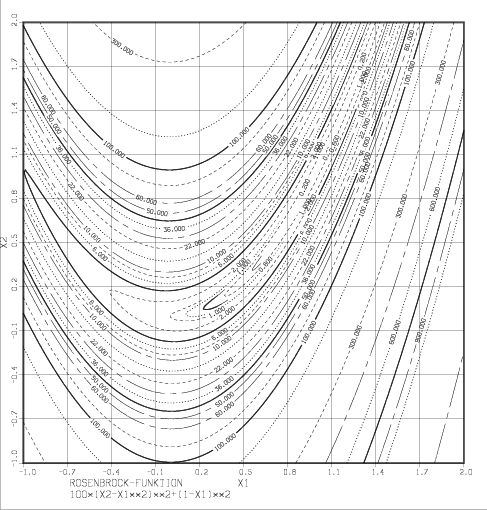
Rosenbrock's banana like valley

$f (x) = 100 (x_{2} - (x_{1})^{2})^{2} + (1 - x_{1})^{2} .$

This is nonconvex but with an unique stationary point (minimizer) at (1,1). Condition number of Hessian there is 2488. The function exhibits a step banana like valley along the parabola $x_{2} = (x_{1})^{2}$ .
Wood's function

$\begin{matrix} f (x) & = & 100 (x_{2} - (x_{1})^{2})^{2} + (1 - x_{1})^{2} + 90 (x_{4} - (x_{3})^{2})^{2} + (x_{3} - 1)^{2} \\ + 10.1 ((x_{2} - 1)^{2} + (x_{4} - 1)^{2}) + 19.8 (x_{2} - 1) (x_{4} - 1) \end{matrix}$

with the unique minimizer $(1, 1, 1, 1)$ . This is also a nonconvex quartic and a combination of two Rosenbrock valley's in the $(x_{1}, x_{2})$ - resp. $(x_{3}, x_{4})$ -plane which are coupled by a convex quadratic in $x_{2}$ and $x_{4}$ . Condition number of the Hessian in the solution is 1400, ( 2766.7353 if measured in the Frobenius norm).
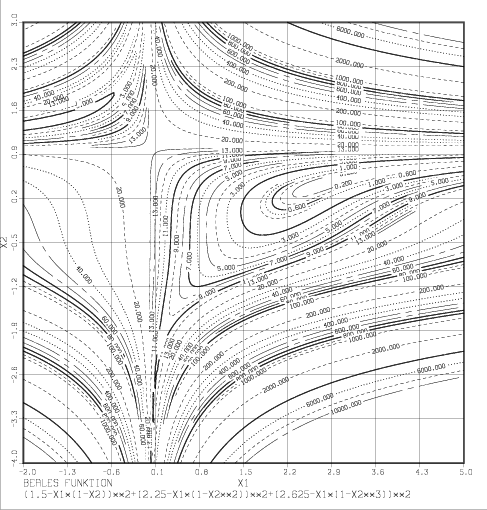
Beale's function

$f (x) = (1.5 - x_{1} (1 - x_{2} {))}^{2} + (2.25 - x_{1} (1 - x_{2}^{2} {))}^{2} + (2.625 - x_{1} (1 - x_{2}^{3} {))}^{2}$

with the unique minimizer $(3, 0.5)$ . This function exhibits a lot of adverse effects: steep growth outside a small strip along the $x_{1}$ -axis, two saddle points at $(0, 1)$ and $(0.100538, - 2.644514)$ and two valleys with $f$ going slowly down as $x_{1}$ resp. $x_{2}$ go to $- \infty$ with the other variable going to zero. Along $x_{1} = 0$ $f$ is constant. Locally the problem is rather well behaved, with a condition of the Hessian being 162.47 in the optimum.
This is obtained from Beale's function by a rescaling (showing bad effects of wrong scaling) by

$x_{1} \to \frac{x_{1}}{100} .$

It has the minimizer $(300, 0.5)$ and otherwise the same (bad) properties as the original function. Condition number of the Hessian in the optimum is now 1440876.9 (measured in the Frobeniusnorm). Although this has two variables only it is already a hard test.
$f (x) = 10000 (x_{2} - (x_{1})^{2})^{2} + (1 - x_{1})^{2}$

This is another modification of Rosenbrock's banana shaped valley, much worse conditioned however. It is obtained by making the valley steeper in replacing the factor 100 by 10000, with the condition number of 250008 at (1,1).
Example of Box: a nonlinear least squares problem with two well separated exponential terms

$f (x) = \sum_{i = 1}^{10} (\exp (- x_{1} i / 10) - \exp (- x_{2} i / 10) - x_{3} (\exp (- i / 10) - \exp (- i {)))}^{2}$

It has the unique minimizer $x_{3} = 1, x_{1} = 1, x_{2} = 10$ . The condition number of the Hessian is 8678.6427 (measured in the Frobeniusnorm).
Fletcher's ''helical valley''

$f (x) = 100 (x_{3} - 10 θ)^{2} + 100 (\sqrt{x_{1}^{2} + x_{2}^{2}} - 1)^{2} + x_{3}^{2}$

with

$θ = {\begin{matrix} \frac{1}{4} for x_{2} x_{1} \to \infty, x_{1} \not = 0 \\ - \frac{1}{4} for x_{2} x_{1} \to - \infty, x_{1} \not = 0, \\ \arctan (x_{2} / x_{1}) / (2 π) for x_{1} \not = 0, \\ \frac{1}{4} for x_{1} = 0 \end{matrix}$

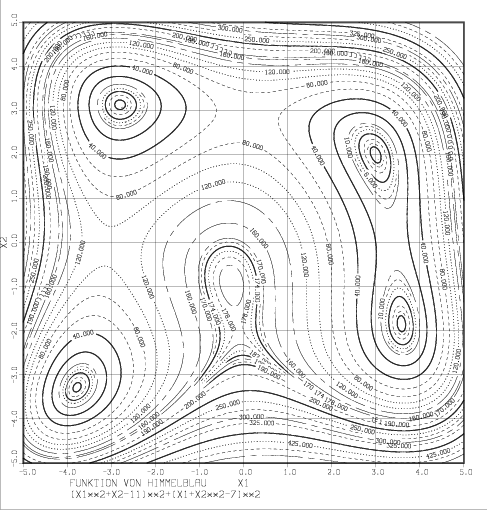
with a minimizer at $(1, 0, 0)$ . The function is discontinuous at $x_{1} = 0$ due to $θ$ but this has no effect locally. Since the initial point is $(- 1, 0, 0)$ one possibly could run into problems depending on details of the stepsize/direction choice, but since the movement will normally be along the unit circle in the $(x_{1}, x_{2})$ -plane this is not probable. The condition number of the Hessian at the solution is 639.97674 .
A function from Himmelblau's collection

$f (x) = ((x_{1})^{2} + x_{2} - 11)^{2} + (x_{1} + (x_{2})^{2} - 7)^{2} .$

This is a quartic with one strict local maximizer, 4 saddle points and four local (and global) minima all with function value 0 ,
1. (3,2)
2. (3.584428,-1.848126)
3. (-3.779310,-3.283185)
4. (-2.805118,3.131313)
These minimizers are well conditioned with condition number of the Hessian less than 4.
Another exponential fit problem

$f (x) = \sum_{i = 1}^{13} w_{i} (y_{i} - (u_{i} x_{1} + \exp (v_{i} x_{2} {)))}^{2}$

with given data for wi , yi , ui and vi . Solution is
```
 fxopt =  .65114732393294D+03
 x(  1)=  .35593023314882D+01 
 x(  2)= -.13414541729370D+00 
 Frobenius-condition of Hessian  = .55144421D+01
```
Since this is a large residual problem but well conditioned, it is a bit harder than Box's example.
An extended function of Rosenbrock type (with variable dimension, here chosen as 100)

$f (x) = \sum_{i = 2}^{100} (100 (x_{i} - x_{i - 1}^{2})^{2} + (1 - x_{i})^{2})$

with the minimizer $(1, \dots, 1)^{T}$ and a condition number like the twodimensional one. Hessian matrix is tridiagonal.

A nonlinear least squares problem of Kowalik and Osborne

f (x) = \sum_{i = 1}^{11} (y_{i} - \frac{x_{1} u_{i} + x_{2} u_{i}^{2}}{x_{4} + x_{3} u_{i} + u_{i}^{2}})^{2}

with given data for

(u_{i}, y_{i}), i = 1, \dots, 11

. Solution is

 fxopt =  .31042260068172D-03
 x(  1)=  .19276545498036D+00 
 x(  2)=  .19385499962955D+00 
 x(  3)=  .12457591209283D+00 
 x(  4)=  .13696937226868D+00 
 Frobenius-condition of Hessian  = .40102216D+04

This is a small residual problem, not quite hard.

Bard's nonlinear least squares fit

f (x) = \sum_{i = 1}^{15} (y_{i} - (x_{1} + \frac{i}{x_{2} (16 - i) + x_{3} (8 - | 8 - i |)}))^{2}

with given data for

y_{i}, i = 1, \dots, 15

. Solution is

 fxopt =  .82148773065790D-02
 x(  1)=  .82410559749789D-01 
 x(  2)=  .11330360920297D+01 
 x(  3)=  .23436951786425D+01 
 Frobenius-condition of Hessian  = .52253693D+04

Nonlinear least squares problem of Brown and Dennis

f (x) = \sum_{i = 1}^{20} ((x_{1} + x_{2} t_{i} - \exp (- t_{i} {))}^{2} + (x_{3} + x_{4} \sin (t_{i}) - \cos (t_{i} {))}^{2})^{2}

with

t_{i} = i / 5, i = 1, \dots, 20

. Solution is

 fxopt =  .60902016845902D+01
 x(  1)=  .74592710503023D+00 
 x(  2)= -.24110360676823D+00 
 x(  3)= -.25812840462753D+00 
 x(  4)=  .44916355421498D+00 
 Frobenius-condition of Hessian  = .72527655D+02

The problem of the hanging chain

\begin{matrix} \int_{0}^{1} y \sqrt{1 + (y^{'})^{2}} d x & \overset{!}{=} & min_{y}, \\ \int_{0}^{1} \sqrt{1 + (y^{'})^{2}} d x & = & L, \\ y (0) = y_{0}, y (1) = y_{1} & . \end{matrix}

This problem first is discretized: the integrals get replaced using the composed trapezoidal rule on a grid of width

Δ x

, but moved by

Δ x / 2

, hence with the quadrature nodes at

x_{i} = (i - 1 / 2) Δ x, i = 1, . . ., N

, with

N Δ x = 1

. Now we have an nonlinear equality constrained minimization problem in the finitely many unknowns

y (x_{1}), \dots, y (x_{N}), y^{'} (x_{1}), \dots y^{'} (x_{N})

. In a second step these values

y (x_{i}), y^{'} (x_{i})

get replaced by the values

y_{i}

y (i Δ x)

using:

y (x_{i}) = (y_{i - 1} + y_{i}) / 2 + O ((Δ x)^{2}), y^{'} (x_{i}) = (y_{i} - y_{i - 1}) / 2 + O ((Δ x)^{2})

resulting in an problem containing only the variables

y_{i}, i = 1, \dots, N

. The total discretization error of this is

O ((Δ x)^{2}) = O (1 / N^{2})

. Now we have a finite dimensional problem

\begin{matrix} f (y) & \overset{!}{=} & min_{y}, \\ h (y) - L & = & 0 . \end{matrix}

Since the gradient of

h

is nonzero everywhere this is finally transformed into an unconstrained problem using Fletcher's smooth exact penalty function

f (y) + (\nabla h (y)^{T} \nabla h (y {))}^{- 1} (- h (y) \nabla f (y)^{T} \nabla h (y) + ϱ (h (y {))}^{2}) \overset{!}{=} min_{y} .

(Since

h

is scalar this has a special form here.) In this example we have chosen

ϱ = 100

and

N = 100

. The problem is already rather illconditioned and because of its strong nonlinearity quite difficult. (Condition number of the Hessian is approx

10^{5}

). Solution is

 fxopt =  .50685050623068D+01
 x(  1)=  .94159104984719D+00 
 x(  2)=  .88666083444093D+00 
 x(  3)=  .83500831458432D+00 
 x(  4)=  .78644444712444D+00 
 x(  5)=  .74079149307301D+00 
 x(  6)=  .69788236709911D+00 
 x(  7)=  .65756002601328D+00 
 x(  8)=  .61967689400482D+00 
 x(  9)=  .58409432252888D+00 
 x( 10)=  .55068208286634D+00 
 x( 11)=  .51931788949949D+00 
 x( 12)=  .48988695255905D+00 
 x( 13)=  .46228155770451D+00 
 x( 14)=  .43640067190022D+00 
 x( 15)=  .41214957364437D+00 
 x( 16)=  .38943950629764D+00 
 x( 17)=  .36818735324255D+00 
 x( 18)=  .34831533368486D+00 
 x( 19)=  .32975071798346D+00 
 x( 20)=  .31242556146702D+00 
 x( 21)=  .29627645576319D+00 
 x( 22)=  .28124429673014D+00 
 x( 23)=  .26727406814124D+00 
 x( 24)=  .25431464033106D+00 
 x( 25)=  .24231858306580D+00 
 x( 26)=  .23124199195329D+00 
 x( 27)=  .22104432775726D+00 
 x( 28)=  .21168826802766D+00 
 x( 29)=  .20313957050418D+00 
 x( 30)=  .19536694779296D+00 
 x( 31)=  .18834195285778D+00 
 x( 32)=  .18203887490668D+00 
 x( 33)=  .17643464529302D+00 
 x( 34)=  .17150875308648D+00 
 x( 35)=  .16724317000505D+00 
 x( 36)=  .16362228443335D+00 
 x( 37)=  .16063284428557D+00 
 x( 38)=  .15826390850419D+00 
 x( 39)=  .15650680701676D+00 
 x( 40)=  .15535510900431D+00 
 x( 41)=  .15480459936514D+00 
 x( 42)=  .15485326328801D+00 
 x( 43)=  .15550127887810D+00 
 x( 44)=  .15675101780888D+00 
 x( 45)=  .15860705400215D+00 
 x( 46)=  .16107618036822D+00 
 x( 47)=  .16416743366724D+00 
 x( 48)=  .16789212758287D+00 
 x( 49)=  .17226389412925D+00 
 x( 50)=  .17729873354286D+00 
 x( 51)=  .18301507284177D+00 
 x( 52)=  .18943383326674D+00 
 x( 53)=  .19657850685092D+00 
 x( 54)=  .20447524239837D+00 
 x( 55)=  .21315294118612D+00 
 x( 56)=  .22264336273999D+00 
 x( 57)=  .23298124107139D+00 
 x( 58)=  .24420441180031D+00 
 x( 59)=  .25635395063007D+00 
 x( 60)=  .26947432368027D+00 
 x( 61)=  .28361355022851D+00 
 x( 62)=  .29882337845616D+00 
 x( 63)=  .31515947484167D+00 
 x( 64)=  .33268162789439D+00 
 x( 65)=  .35145396697468D+00 
 x( 66)=  .37154519700103D+00 
 x( 67)=  .39302884990335D+00 
 x( 68)=  .41598355374263D+00 
 x( 69)=  .44049332048187D+00 
 x( 70)=  .46664785346166D+00 
 x( 71)=  .49454287570561D+00 
 x( 72)=  .52428048025719D+00 
 x( 73)=  .55596950383027D+00 
 x( 74)=  .58972592514080D+00 
 x( 75)=  .62567328937754D+00 
 x( 76)=  .66394316036530D+00 
 x( 77)=  .70467560207567D+00 
 x( 78)=  .74801969124733D+00 
 x( 79)=  .79413406299239D+00 
 x( 80)=  .84318749138523D+00 
 x( 81)=  .89535950715910D+00 
 x( 82)=  .95084105477097D+00 
 x( 83)=  .10098351912395D+01 
 x( 84)=  .10725578293138D+01 
 x( 85)=  .11392385276930D+01 
 x( 86)=  .12101213311882D+01 
 x( 87)=  .12854656639030D+01 
 x( 88)=  .13655472787000D+01 
 x( 89)=  .14506592664292D+01 
 x( 90)=  .15411131286118D+01 
 x( 91)=  .16372399175053D+01 
 x( 92)=  .17393914477220D+01 
 x( 93)=  .18479415838362D+01 
 x( 94)=  .19632876086917D+01 
 x( 95)=  .20858516774181D+01 
 x( 96)=  .22160823624770D+01 
 x( 97)=  .23544562953935D+01 
 x( 98)=  .25014799111804D+01 
 x( 99)=  .26576913018410D+01 
 x(100)=  .28236621857326D+01

Reserved for user defined function.

File translated from T_EX by T_TM Unregistered, version 4.03.
On 16 Jun 2016, 15:59.