Ein verbessertes Nelder-Mead-Verfahren

• Das Nelder-Mead-Verfahren ist ein sogenanntes ''ableitungsfreies'' Minimierungsverfahren, das nur Funktionsauswertungen benötigt. Es ist zwar beweisbar nicht immer konvergent (McKinnon SIOPT 1998), aber bei den Anwendern das bei weitem beliebteste, wohl wegen seiner Einfachheit und auch weil es ''meistens'' recht gute Ergebnisse liefert, jedenfalls wenn die Dimension des Problems klein ist. Das Originalverfahren wurde von Nelder und Mead (Computer Journal 7, (1965),308-313) veröffentlicht. Hier wird eine beweisbar konvergente Modifikation von A. Witzel (Dissertation, 2008) benutzt.
• In jedem Schritt des Verfahrens liegt ein Simplex im Rⁿ vor, also die konvexe Hülle von n+1 affin unabhängigen Punkten xⁱ, i=0,...,n, an denen die Funktionswerte f(xⁱ) bekannt sind. Ein Schritt des Verfahrens erzeugt einen neuen Simplex so, dass der grösste Funktionswert auf den Ecken dieses neuen Simplex kleiner ist als der grösste Funktionswert auf dem zuvor berechneten. Dies geschieht durch eine Anwendung von Modifikationsregeln. Zu einem Simplex mit den Ecken xⁱ, i=0,...,n sei definiert
  
  1. f_h = max { f(x^j): j=0,...,n }, der grösste f-Wert
     
  2. H = { i: f(xⁱ) >= f_h - epsf*rho }, die Indexmenge der grossen f-Werte
     
  3. L = { 0,...,n}\ H, die Indexmenge der kleinen f-Werte
     
  4. f_l = argmin{ f(xⁱ), i=0,...,n }, der kleinste f-Wert
     
  5. f_s = min { f(xⁱ) : i in H }, der kleinste unter den grossen f-Werten.
     
  epsf ist ein Verfahrensparameter, der in den ''Hauptzyklen'' des Verfahrens fest ist und beim Abbruch eines Hauptzyklus um einen festen Faktor verkleinert wird. rho ist die grösste Kantenlänge im laufenden Simplex. Ferner ist
  xs = 1/|L| Summe_{i in L} xⁱ .
  also der Schwerpunkt der Ecken mit ''niedrigen'' Funktionswerten. Man hat Verfahrensparameter α >0, γ > 1 und 0 < β < 1 und 0 < δ < 1, den Reflektionskoeffizienten, den Expansionskoeffizienten, den Kontraktionskoeffizienten und den Koeffizienten der massiven Kontraktion. Typische Werte sind
  α = 1 , β = 0.5, γ = 2, δ = 0.5
  
• Ist L leer, dann wird zunächst entlang der Simplexkanten von einem x^l aus durch eine Gittersuche mit Verfeinerung um den Faktor δ nach einem Funktionswert gesucht, der kleiner ist als
  f_h-epsf*rho*δ^m mit m=0,..., wobei in beiden Richtungen gesucht wird. Dies wird hier als ''symmetrische massive Kontraktion'' bezeichnet, ''smsc''. Wird kein solcher Wert gefunden, dann werden epsf und rho um einen festen Faktor verkleinert. Unterschreiten dabei beide Werte eine vorgegebene untere Schranke (hier 10^-14 und 10^-15) dann bricht das Verfahren ab: man hat zumindest einen stationären Wert von f in x^l (näherungsweise). Sonst wird neu gestartet, d.h. die Indexmengen werden neu bestimmt. In unmittelbarer Nähe eines Minimums kommt es immer zwangsläufig zu smsc-Schritten. Weitere Abbruchgründe sind: Änderung von f kleiner als epsfmin und Simplexdiameter kleiner als diameps, Simplexdiameter kleiner als diammin, Simplexdiameter grösser als diammax, mehr als maxiter Schritte erforderlich, mehr als 10 aufeinanderfolgende geringe Änderungen in f.
• Ist nun L nicht leer, dann wird versucht, alle Punkte aus H durch bessere Werte zu ersetzen, wobei es genügt, Werte kleiner als f_h zu erhalten. Folgende Operationen sind vorgesehen, die nacheinander für jeden Punkt aus H ausgeführt werden:
  1. Der Reflektionsschritt. Definiere
     x^r = (1+α) xs - α xⁱ für i in H .
     x^r liegt also auf der Geraden durch xⁱ und xs , den Schwerpunkt der Punkte in L , jedoch auf der xⁱ gegenüberliegenden Seite zu xⁱ. Drei Fälle können bei der Reflektion auftreten:
     1. f(x^r) < f(x^l) . In diesem Fall wird ein Expansionsschritt ausgeführt.
     2. f(x^l) <= f(x^r) < f(x^s). In diesem Fall wird x^h durch x^r ersetzt und ein neuer (Teil-)Schritt des Verfahrens gestartet.
     3. f(x^s) <= f(x^r). In diesem Fall wird unterschieden: ist f(x^r) < f(x^h), so wird x^h durch x^r ersetzt und anschliessend ein Kontraktionsschritt ausgeführt (s.u.). Andernfalls wird sofort ein Kontraktionsschritt ausgeführt. Sei dazu
        f(x^h') = min {f(x^r),f(x^h) }
        
  2. Der Kontraktionsschritt. Der Kontraktionspunkt x^c ist definiert durch
     x^c = β x^h'+(1-β) xs
     β ist das Verhältnis der Abstände ||x^c- xs|| und ||x^h' - xs||. Nach Definition von h' ist also
     x^c = β x^h +(1-β)xs wenn f(x^r) >= f(x^h) (innere Kontraktion)
     bzw.
     x^c = β x^r +(1-β)xs wenn f(x^r) < f(x^h).
     (äussere Kontraktion) Ist nun f(x^c) < f(x^h), so wird x^h durch x^c ersetzt und der nächste Schritt wird begonnen, andernfalls wird eine massive Kontraktion ausgeführt.
  3. Die massive Kontraktion. In diesem Fall werden für i ungleich l alle Punkte durch
     xt ⁱ = x^l +(-) δ^m (xⁱ-x^l)
     ersetzt, bis alle neuen Simplexpunkte kleinere Werte als f_h aufweisen. Diese massive Kontraktion tritt vor allem in zwei Situationen auf: x^h befindet sich in der Nähe eines Sattelpunktes und die Reflektion wird in Richtung eines Anstieges ausgeführt oder die Niveaubereiche von f sind sehr stark gekrümmt und f(x^h) ist sehr viel grösser als alle anderen Funktionswerte.
  4. Der Expansionsschritt. Dieser Schritt wird ausgeführt, wenn f(x^r) < f(x^l). Man kann dann hoffen, in der Richtung von x^h nach x^r noch kleinere Werte von f zu finden. Man setzt
     x^e = γ x^r+(1-γ) xs
     Ist f(x^e) < f(x^r), dann wird x^h durch x^e, sonst wird x^h durch x^r ersetzt und der Algorithmus neu gestartet.
• Bei diesem Algorithmus werden also pro Schritt (pro neuem Simplex) ein, zwei oder maximal 2mn neue Funktionswerte berechnet, letzteres nur im Falle der massiven Kontraktion oder wenn L leer war. Es kommt vor, dass der Simplex entartet, d.h. die Ecken werden affin abhängig. Dies wird mittels der QR-Zerlegung der Simplexmatrix kontrolliert und durch Neuaufbau eines entarteten Simplex (in den Richtungen der Q-Matrix) behoben. Um den Aufwand ertr"aglich zu halten, wird der Diagonalteil der R-Matrix zur Konditionsschätzung benutzt. Auch bei diesem Neuaufbau wird durch Gittersuche sichergestellt, dass der maximale Funktionswert im Simplex immer monoton fällt. Der Parameter condbound im Eingabeteil ist eine Schranke, die man für diese Konditionsschätzung vorgibt.

Die Eingaben

• Sie haben die Wahl zwischen 14 vorgegebenen Funktionen, zu denen Sie auch eine genauere Beschreibung nachlesen können. Oder Sie geben eine eigene Funktion f, abhängig von n Variablen x(1),...,x(n), und die Startwerte zu diesen Variablen an.
• Sie können entweder Standardparameter wählen oder eigene Kriterien angeben.
  (Standardparamater sind in die Felder eingetragen) Die Bedeutung der Parameter ist im Eingabeformular angegeben.
• Für die festeingestellten Funktionen ist noch eine Angabe der Startwerte der Variablen möglich, wobei Sie auch hier eine Standardinitialisierung wählen können. Sie finden die jeweilige Anzahl n der Variablen bei den Kurzbeschreibungen oben im Eingabeformular.
• Des weiteren haben Sie die Wahl, ob Sie einen Höhenlinienplot als Ausgabe möchten. Wenn ja, dann werden noch die Indices der beiden Variablen, bezüglich derer das Bild geplottet werden soll, sowie entsprechende Intervallangaben benötigt. Bei der Berechnung der Höhenlinien werden die anderen Variablen auf den berechneten Optimalwert gesetzt.

Die Ausgaben

• CPU-Zeit, Name des Testfalls und eine Statistik über die ausgeführten Schritte. Hier bedeutet ''Hcnt=1'' dass ein unmodifizierter Nelder-Mead-Schritt (Originalverfahren) vorlag.
• Den Grund des Rechnungsabbruchs.
• Die berechneten Optimalwerte f(x_opt) und x(1)_opt,...,x(n)_opt und den sogenannten ''Simplexgradienten'', also eine Näherung an den Gradienten von f aufgrund der Funktionswerte auf den n+1 Ecken des letzten Simplex.
• Wenn Sie ein Protokoll des Iterationsverlaufs gefordert haben, wird eine Liste angezeigt mit Iterationsschritt, maximalem Funktionswert im Simplex (streng monoton fallend), dem Simplexdiameter und dem Typ des Ersetzungsschrittes. Dabei bedeutet ''refl'' Reflektion, ''exp'' Expansion, ''i_contr'' innere und ''o_contr'' äussere Kontraktion sowie ''msc'' massive Kontraktion. Die Sonderschritte ''smsc'' und Simplexneuaufbau werden angezeigt.
• Vier Plots: Logarithmus des Fehlers f - f_opt, die Anzahl der aufgewendeten Funktionsauswertungen (in der Regel strikt linear in der Schrittzahl und dies unabhängig von n), maximaler Simplexdiameter (woran man die Dynamik des Verfahrens gut ablesen kann), und Schritttyp: 1 steht für Reflektion, 2 für Expansion, 3 für äussere und 4 für innere Kontraktion, 5 für massive Kontraktion. Die um 5 erhöhten Werte stehen für die gleichen Schritte nach einer symmetrischen massiven Kontraktion und die um 10 erhöhten nach einem Simplexneuaufbau.
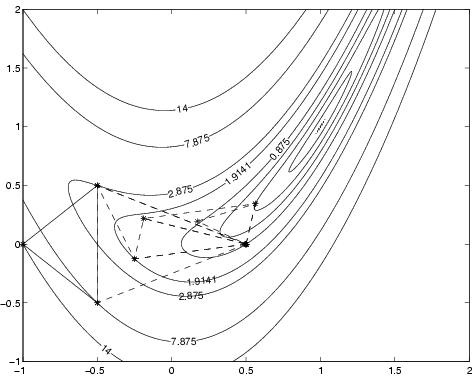
• Und den Höhenlinienplot, falls Sie diesen gewünscht hatten.

Das Eingabeformular

Zurück: Unrestringierte Minimierung